 |
| Home > Geometry > Topology |
Knot theory
Knot theory is an area of topology full of unsolved problems. Most things that non-mathematicians would consider knots are not, the difference being that mathematical knots are impossible to untie without cutting. For this reason, mathematicians often join the ends into a loop. Apart from the trivial unknot (an unknotted circle) there are many knots. The simplest is the trefoil knot. However, there are many more. The simplest family of knots is the "foil" family. It contains an infinite number of knots, and is a subset of the torus knot family. Here are some pictures.
 |
| Trefoil knot 31 |
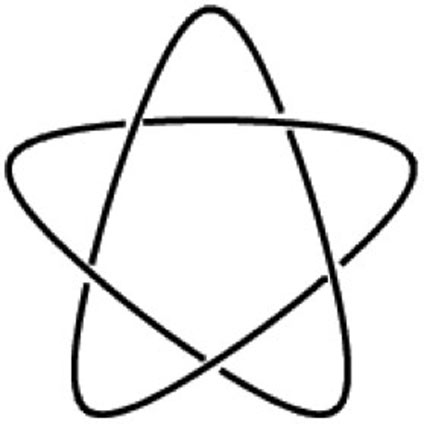 |
| Cinquefoil knot 51 |
 |
| Septafoil knot 71 |
There are also other families of knots. There are twist knots. The first of these is the trefoil again but every other knot is new.
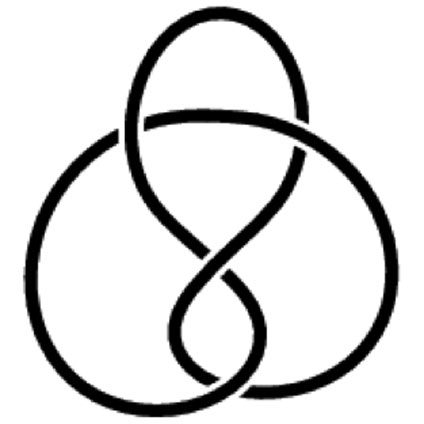 |
| Figure-of-8 knot 41 |
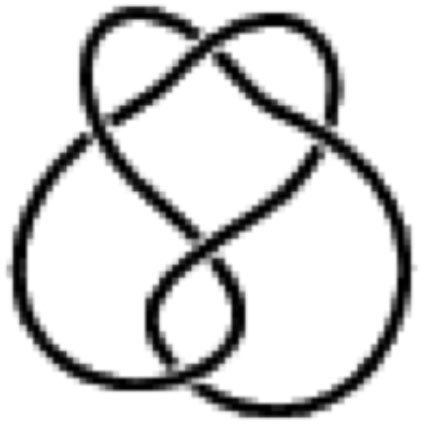 |
| Three-twist knot 52 |
 |
| Stevedore knot 61 |
How do you tell if two knots are different? First we need to define the permitted ways of deforming a knot. There are three, classified by Kurt Reidemeister, called the Reidemeister moves.
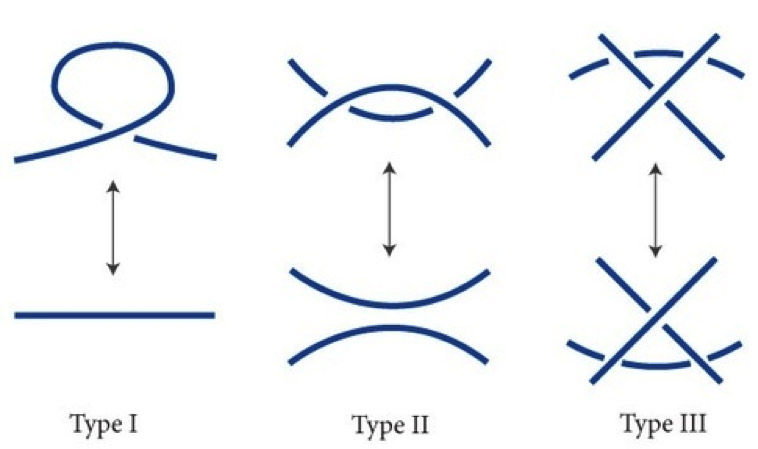 |
| Permitted ways of modifying a knot -- the Reidemeister moves
|
The first move can be called a twist (or untwist), the second a poke (or unpoke), and the third a slide (not unslide as that is just another slide). Now we can define invariants. One of the simplest is 3-colouring. Colour each line segment of the diagram in one of three colours. A knot is 3-colourable if there exists a colouring which satisfies the following:
1: At any crossing, there is an overpass and two underpasses. For each crossing, the three colours involved must either be all the same or all different.
2: At least two colours are used.
It can be shown that this does not change when a Reidemeister move is applied. The unknot cannot be coloured as it would only use one colour. However, the trefoil knot can be 3-coloured. There is a generalisation for n colours:
Label each line segment with an integer modulo n.
1: At any crossing, there is an overpass and two underpasses. For each crossing, twice the overpass's number must be congruent to the sum of the underpass numbers modulo n.
2: At least two numbers are used.
This can tell many knots apart but not all. The trefoil has a mirror image which cannot be deformed to make the original. The square knot and the granny knot are also distinct. However, colourability cannot tell them apart. However, there is a polynomial called the Jones polynomial which can do this and tell many more of the trickier knots apart. There also exists an even more powerful polynomial called the HOMFLY polynomial. However, none of these have been proven to be complete invariants, which means that there may be distinct knots which they cannot tell apart.
Related entries
• Möbius band
• Topology