February 2015 - Circles Inside Circles (Solution)

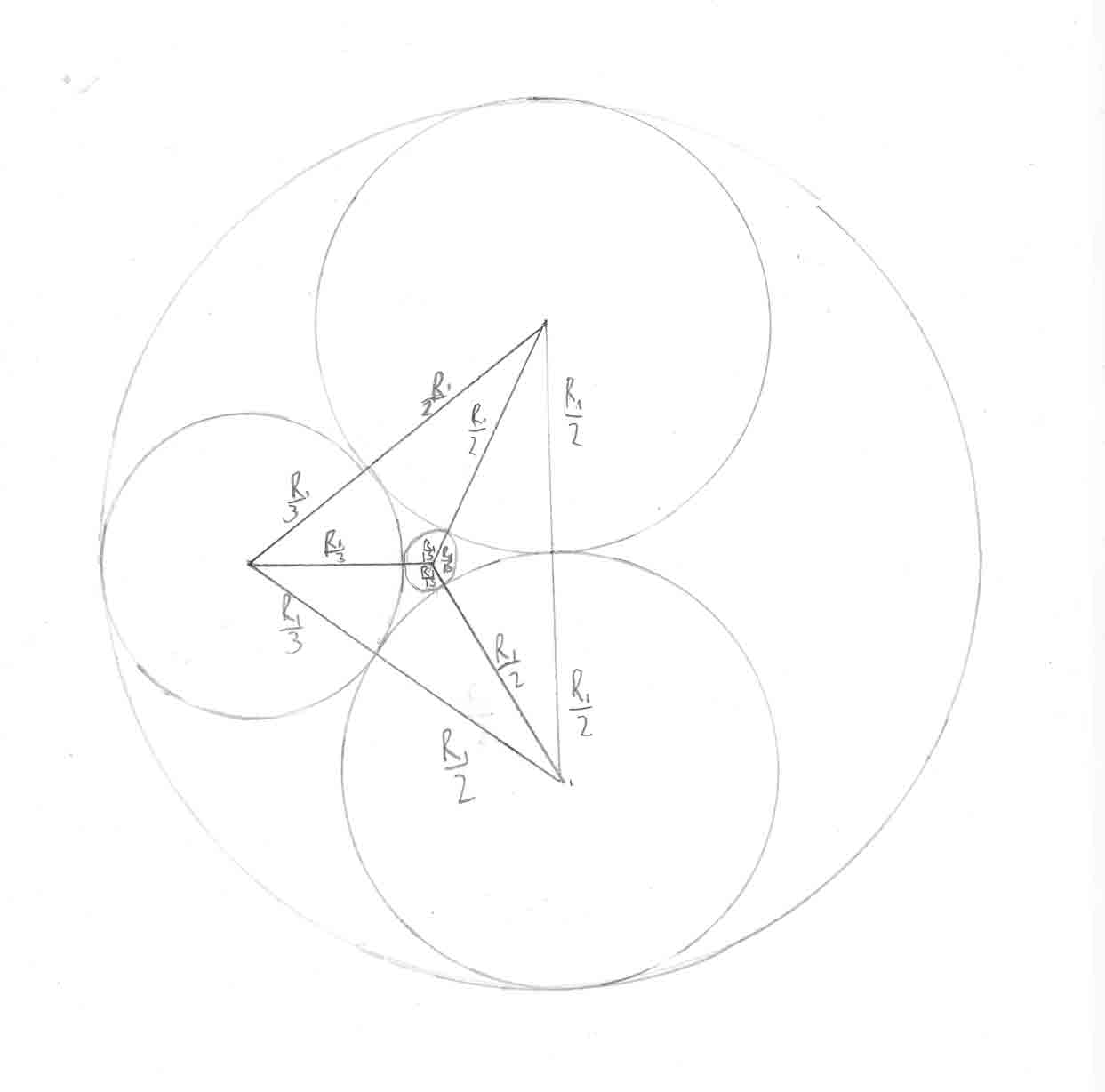
The answer is 225. Let the largest circle have radius R₁. The next largest circles have radius R₁/2. The second smallest circle's radius must be found using Pythagoras' theorem. Make a triangle with the centres of these circles: The largest circle, one of the next largest circles, and the second smallest circle. Let the second smallest circle have radius R₂. The horizontal side length is R₁- R₂. The vertical side length is R₁/2. The hypotenuse has length R₁/2+R₂. Thus (R₁- R₂)²+R₁²/4=(R₁/2+R₂)². Expanding, R₁²- 2R₁R₂+ R₂²+ R₁²/4=R₁²/4+ R₁R₂+ R₂². Subtracting R₁²/4 - 2R₁R₂+ R₂², we have R₁²=3R₁R₂. Thus R₁=3R₂ and R₂=R₁/3. Consider another right-angled triangle with the centres of these circles: The largest circle, one of the second largest circles, and the smallest circle. Let the smallest circle have radius R₃. The vertical side is the same. The horizontal side has length R₁-2R₂- R₃. The hypotenuse has length R₁/2+R₃. Solving in a similar manner to the previous step, R₃=R₁/15. Now, the smallest circle has area πR₁²/225=1. Thus πR₁²=225. However, the largest circle has area πR₁². Thus the largest circle has area 225.

Related entries