April 2015 - Hexagons Inside Hexagons (Solution)

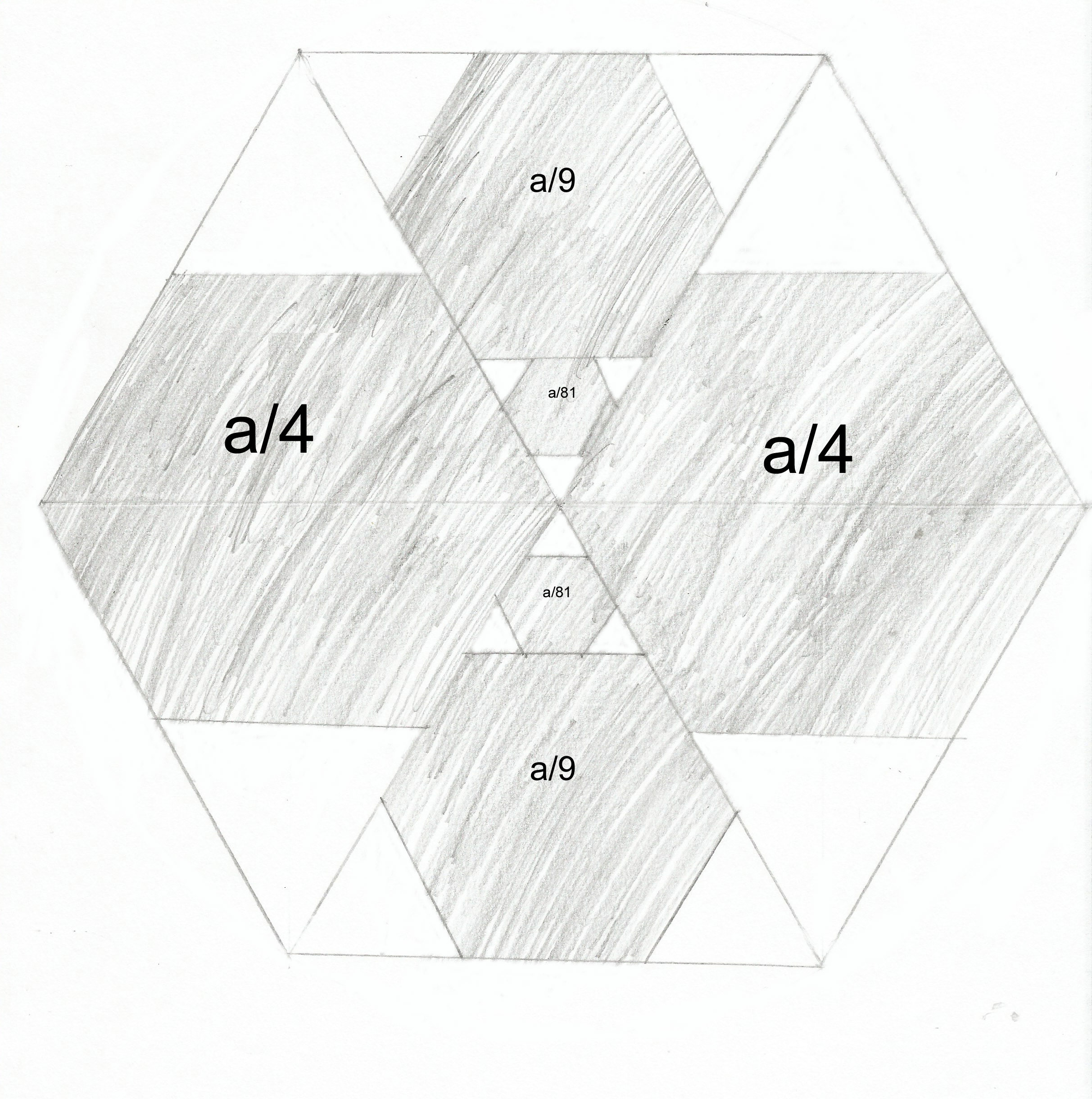
(I apologise for the fact that in this image, I have somehow reversed the shaded and unshaded areas) The answer is 121. Let the side length of the largest hexagon be s and let its area be a. All regular hexagons are similar so their area is proportional to the square of their side length. The length of the long diagonal of the larger hexagons is half of the length of the long diagonal of the largest hexagon. Thus the side length of the larger hexagons is s/2 and the area is a/4. Now split the largest hexagon into six equilateral triangles. The smaller hexagons fit inside an equilateral triangle of side length s so, by dividing it into equilateral triangles of side length s/3, it is possible to show that the smaller hexagons have side length s/3 and area a/9. The smallest hexagons are similar, except that they are in a triangle with side length s/3 and thus have side length s/9 and area a/81. Adding all the areas shows that the total shaded area is 121a/162 so the unshaded area is 41a/162, which is given to be 41. Thus a = 162 so the total shaded area is 121.

Related entries