 |
| Home > Geometry > Abstract geometry |
Finite projective planes
When thinking about geometry, most people reason by spatial intuition
from what they see in the real world. Thus we know what a line and point
"look like". However, abstract geometry does not necessarily
follow that. In abstract geometry, it does not matter what points and
lines really look like, only that they follow certain rules called axioms.
Thus in abstract geometrical configurations a line may not look like a
straight line.
First, before any work can be done, it is necessary to create a list of axioms. These axioms are assumed in the context of the geometry. Changing the axioms will give you different types of geometries. Before even that, some definitions are required. Since everything must only be defined in terms of other objects in the geometry, it is necessary to leave some things undefined. For example, we don't care about what a point really is, only that it obeys all axioms for points. Thus points will be left undefined. It is possible and convenient in many cases to consider a line as a set of all points on it. This leads to three definitions:
D1: A line is a set of points.
D2: A point lies on a line if the point is an element of the line.
D3: A line contains a point if the point lies on the line.
Now we have some basic definitions, it is necessary to decide on axioms. Firstly, every two points should be joined by a line. Secondly, every two lines should meet at a point. This axiom is not true in Euclidean geometry as parallel lines do not meet, but in projective geometry there are no parallel lines. If there were parallel lines, the plane would be known as an affine plane. The Euclidean plane is an example of an affine plane but not a projective plane. Thirdly, we want to exclude certain trivial geometries which are not of interest to us. An example of a trivial geometry is a single line with arbitrarily many points on it. These trivial geometries lack many of the structures that projective geometries have, and many theorems fail to hold for them. There are three commonly accepted axioms:
A1: For any two distinct points, there is exactly one line that contains both points.
A2: For any two distinct lines, there is exactly one point that lies on both lines.
A3: There exist four distinct points, no three of which lie
on the same line.
A1 and A2 determine that every two points are joined by a line and every two lines meet at a point, while A3 rules out trivial geometries. These three axioms are enough to prove many theorems. Firstly, some notation is helpful. A point is a capital letter. A line is denoted by at least two of the points on it. For example, LAB is the line containing A and B. It is possible to prove that every projective plane has at least 7 points. Here is the proof:
Let A, B, C, D be four distinct points such that no three of them lie on the same line. Their existence is implied by A3. Now, by A2, LAB and LCD meet at a point. Let this point be E. E cannot be A as if E were A, A would lie on LCD which would contradict the assumption that A, C, and D do not lie on the same line. Similarly, E cannot be B, C, or D. Likewise, LAC and LBD meet at F, which cannot be A, B, C, or D and LAD and LBC meet at G, which cannot be A, B, C, or D. Suppose E and F were identical. Then LAB and LAC both contain E (as LAC contains F). However, by A1, there is exactly one line containing both A and E. This line must therefore also contain B and C. However, this contradicts the assumption that A, C, and D do not lie on the same line. Thus E is not F. Likewise, E is not G and F is not G. Thus the points A, B, C, D, E, F, and G are all distinct so the plane has at least 7 points.
A more complex theorem shows that there exists a number n such that each point lies on exactly n+1 lines and each line contains exactly n+1 points. In this case n is known as the order of the projective plane. It is possible to optionally define a fourth axiom that determines the order of the plane:
A4(n): Every point lies on exactly n+1 lines and every line contains exactly n+1 points.
This axiom is used if you want to only consider planes of a certain order. It can be omitted if you want to consider all projective planes. Firstly, no plane has order 1. This can be shown as in the previous example there were lines containing 3 points and points on 3 lines, which is not allowed in a plane of order 1. However, consider A4(2). Assume this was true. Now consider the construction proved to exist in the previous theorem. We have points A, B, C, D, E, F, G and lines LABE, LACF, LADG, LBCG, LBDF, and LCDE. Now, consider LEF. This must have another point by A4(2). Also, by A2, there must be at least one point lying on both LEF and LADG. Now, since LADG contains exactly 3 points, the point lying on both LEF and LADG must be A, D, or G. Now, LABE contains both A and E. If LEF contained A, it would be identical to LABE by A1 and thus contain B. However, it now contains 4 points which contradicts A4(2). Likewise, if LEF contained D, it would also contain C, which contradicts A4(2). Thus LEF contains G. If there were another point H and the line LAH did not correspond to any line already containing A, there would be 4 lines through A, which contradicts A4(2). However, if the line LAH was already one of the lines through A, that line would have 4 points, which contradicts A4(2). Thus there can be no more points. Thus the unique projective plane of order 2 consists of points A,B, C, D, E, F, and G and lines LABE, LACF, LADG, LBCG, LBDF, LCDE, and LEFG.
This plane of order 2 is known as the Fano plane after Gino Fano who first described it in 1892. He also described a 3-dimensional projective geometry called the Fano 3-space where every plane was a Fano plane. The Fano plane is the smallest projective geometry and has many applications. For example, it is used in the construction of the Hamming code in information theory. It also represents the 7 basic imaginary octonions, where two octonions multiply to make the third in the same line. Using a directed graph can determine whether the product is positive or negative.
Despite the abstract nature of these constructed geometries, it is possible to draw a graph representing them. However, such a graph may have counterintuitive properties. For example, many apparent "points" actually do not exist and lines may not look like straight lines. Here is a diagram of the Fano plane:
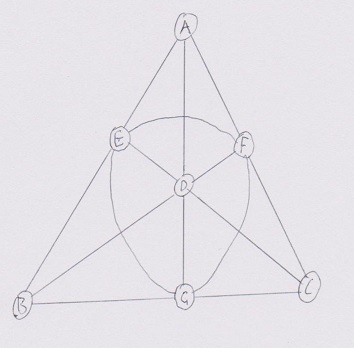
It is also possible to define higher geometries such as projective 3-spaces, the simplest being the Fano 3-space. Slightly different axioms apply here but many principles are similar. Here an advantage of the axiomatic method shows. It is possible to define spaces in 4 or more dimensions, even though they do not appear in our physical world and are difficult to grasp intuitively.
It is also possible to classify all finite projective planes of small orders. The Fano plane is the unique projective plane of order 2. There is exactly one projective plane of orders 3, 4, 5, 7, and 8. It was proved in 1901 by Gaston Tarry that there is no projective plane of order 6. There are exactly 4 projective planes of order 9. After intensive computer calculation, it was proved that no projective planes of order 10 exist. There is only one known projective plane of order 11 but others may exist. It is conjectured that there are no projective planes of order 12.