Four dimensional space

The 19th century mathematics Charles H. Hinton trained himself to visualise four dimensions

A two-dimensional projection of a tesseract

It is easy to visualise space in 3 dimensions. That is because we live iin it and evolved to be able to visualise it. However, mathematicians can do geometry in 4, 5, or even infinitely many dimensions. A trick is to use coordinates. Every point in 2D space can be represented as a pair of coordinates. Likewise, every point in 3D space can be represented with 3 coordinates. Now imagine a point with 4 coordinates. That point is in 4D space.

There are various ways to visualise it. One is to imagine the fourth dimension as time. (Do NOT mix this up with space-time, which has a different treatment of time compared to the three spatial dimensions). Another is to visualise three-dimensional models. This seems impossible until you realise that it is possible to make two-dimensional drawings. This gives a projection which can be used to reason about the 3D object. However, the most useful tool is reasoning by analogy.

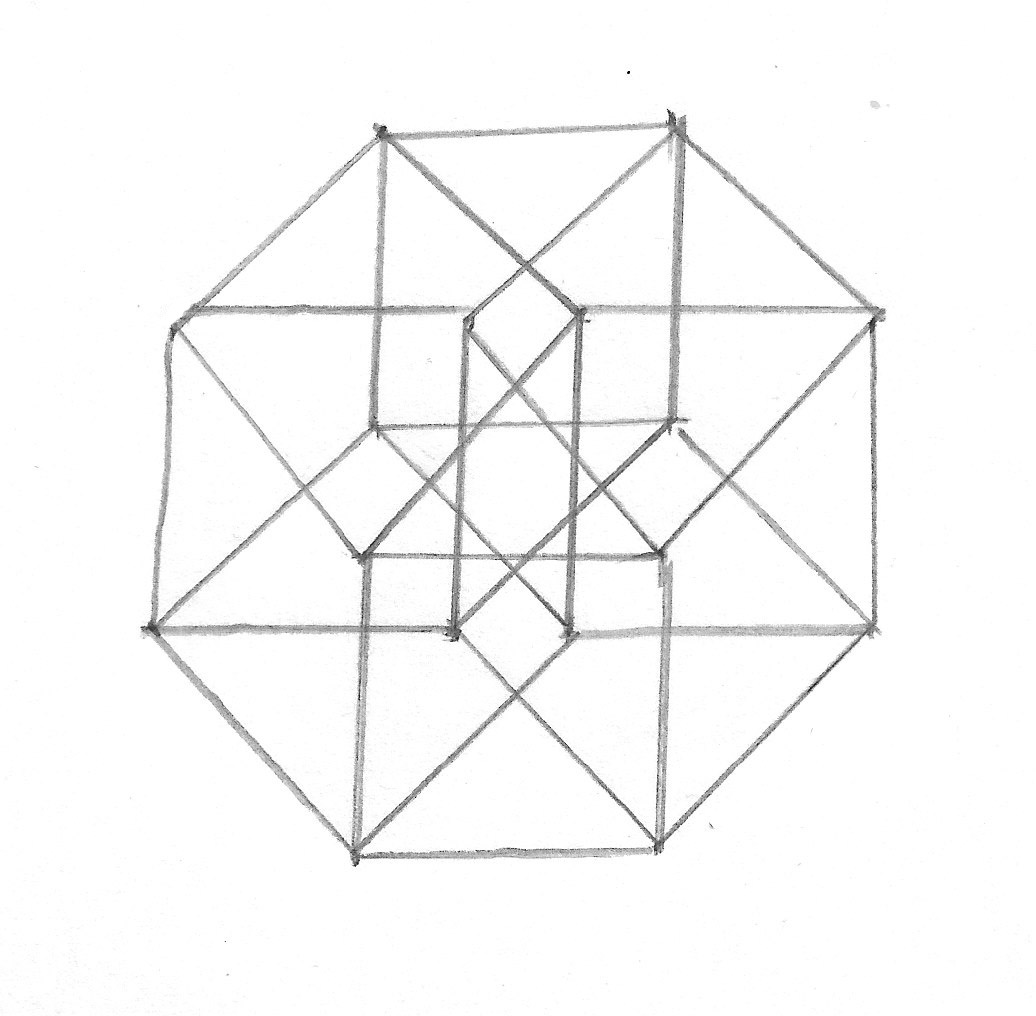
First, the 4D equivalent of a cube is called a tesseract. To visualise it, imagine two squares. One is further along in the third dimension. Joining them up, you get a cube. Likewise, join two cubes to get a tesseract. This can actually be drawn on paper just as you can draw a cube. This has 16 vertices, 32 edges, 24 faces, and 8 "cells", which are 3D versions of faces. It is a mistake to think that if yu made a tesseract and trapped a four-dimensional beast inside it then made the faces solid, the beast couldn't escape. In actual fact, it could escape through a cell. This is like trying to trap a three-dimensional being inside a cube by making the edges solid. However, in the 4D case, if you make the cells solid, the beast will be trapped inside.

There are other polychora (four-dimensional solids) named after the number of cells. The first polychoron is the 5-cell, an analogue of the triangle and tetrahedron. This has 5 tetrahedral cells, 10 triangular faces, 10 edges, and 5 vertices. It is poossible to find the "dual polychoron" by replacing cells with vertices, faces with edges, and vice versa. The dual of a 5-cell is another 5-cell. Then you have the 8-cell (tesseract). There is also a 16-cell, which is the dual of the tesseract and the analogue of the octahedron. This has 16 tetrahedral cells, 32 triangular faces, 24 edges, and 8 vertices. Two other polychora are the 120-cell, an analogue of the dodecahedron, and the 600-cell, an analogue of the icosahedron. Finally, there is a 24-cell, a polychoron which is actually a self-dual. It has 24 octahedral cells. This has no good analogue in 3 dimensions.

Then there are 3-spheres. This refers only to the dimension of the surface. Thus an ordinary sphere is a 2-sphere. Now, the 3-sphere has a 4-volume which is the 4-dimensional equivalent of area or volume. If the radius is r, the 4-volume is π²r⁴/2. Also, the surface volume is given by 2π²r³. The algebraic formula is analogous to a circle or sphere: x²+y²+z²+w²=r². However, this is actually a finite 3-dimensional space.

There are also analogues of cylinders. A cylinder is a circular prism, which is a circle extended in the third dimension. It can also be seen as a shape between a cube and a sphere. There are 3 such cylinders in the fourth dimension. The first is the cubinder, which is a cylinder extended along the fourth dimension. Then there is a spherinder, which is a spherical prism. Finally, there is a duocylinder, which is rather different. If a cylinder is a line moved in a circle this is a circle (2 dimensions) moved in a circle (the other 2 dimensions).

Related entries