 |
| Home > Cellular automata > Life |
Life with ordinals
The game of Life (as defined by J. H. Conway) goes as follows:
1: There is a square grid of cells, and each can either be black or white.Many complex patterns arise out of these simple rules. There are oscillators, which repeat after a fixed time period. The simplest is called the blinker and is shown as follows:
2: The neighbours of a cell are the 8 cells orthogonally and diagonally adjacent.
3: In the next frame, a black cell turns white iff the number of black neighbours is 0, 1, 4, 5, 6, 7, or 8.
4: In the next frame, a white cell turns black iff there are exactly 3 black neighbours.
0: 
1: 
2: (0)
This keeps on repeating. However, it becomes far more complex if we allow ordinals. The first ordinal is ω and any square which is black infinitely many times in the natural number sequence is black.ω:

ω+1: 
ω+2: 
ω+3: 
ω+4: 
ω+5: 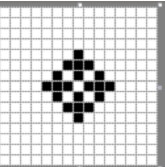
ω+6: 
ω+7: 
ω+8: (ω+6)
So you might think “Why not just plot the cross in the first place
to trace the blinker’s entire history?” The answer is that
we can now go to ω*2 (with a fundamental sequence of ω+n)
and use the same rule as before. A cell is black in any limit ordinal α
iff the set of ordinals below α in which the cell is black has supremum α.
This could lead to complexities that Conway could not
have even imagined when he first invented Life.
ω*2: 
ω*2+1: 
...
ω*3: 
ω*4: 
From here onwards the patterns get huge... up to a point. That point is
ω*5+25. At this stage the transfinite blinker has produced 8 blocks,
4 beehives, and requires a 31 by 31 grid to show. If every intermediate
step is shown as well, a 33 by 33 grid is needed.
Some oscillators are simpler. The beacon always remains a beacon and never
stabilises. The toad becomes a block at ω+3. However, other patterns
may become more and more complex, requiring ever large r ordinals to stabilise.
We can also consider patterns that are not oscillators. Basic spaceships such as the glider disappear instantly at ω. However, the Gosper glider gun is a different story. At ω it becomes an infinite diagonal stream headed by a mass of black cells where the actual gun was. This makes it more difficult to analyse.
I have still not found a pattern that stabilises at ω2 or beyond. I have, however, found a class of hypothetical patterns, known as ω-spaceships. At ω they would repeat the original pattern but shifted by a few cells. These will take up to at least ω2 to stabilise. However, none are known as of yet. If you do find one, let me know.
You could technically go further but it would seem completely intractable until a pattern stabilising at at least ω2. How large is it possible to get to? I conjecture strongly that the ordinal of any pattern is countable, although I do not have a proof as of yet. I also conjecture (but not as strongly) that all patterns have an ordinal below the Church-Kleene ordinal (the ordinal that, in the fast-growing hierarchy, matches the Busy Beaver function), due to Life simulating a universal Turing machine. My third conjecture is that all ordinals below the Church-Kleene ordinal (or ω1, in case my second conjecture is false) can be achieved or surpassed by a pattern.