Ramsey theory

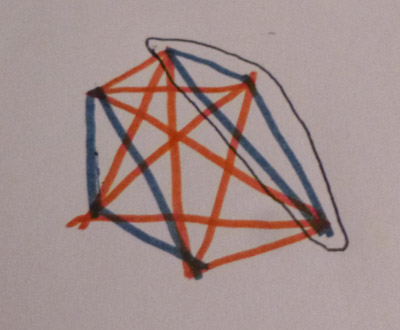Six nodes, showing one triangle of the same colour

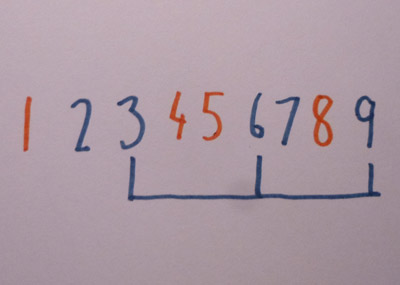Numbers from 1 to 9, with an arithmetic sequence of length 3

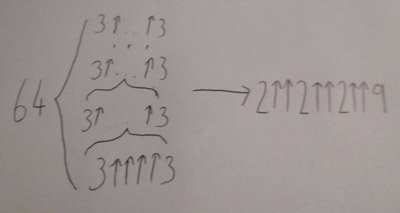Illustration showing the improvement in the upper bound to Graham's problem

Ramsey theory is a branch of mathematics. Essentially, it asks how big an arbitrary set is before some particular pattern must occur. It is named after Frank Ramsey, an English mathematician. There are many questions that can be asked, but one of the main ones is the party problem. A modern interpretation makes it less ambiguous. Given six users of Facebook, is it always possible to find three such that either all are friends or none are friends? (The reason I used Facebook is that this avoids any ambiguity about whether being friends is symmetric. With Facebook it is unambiguously symmetric.) This is a simple problem in Ramsey theory. In fact, the proof is constructive. Take one person. They will either have three or more friends among the six users or two or less. If they have two or less, they will have three or more non-friends. Suppose they have three or more friends. (The situation with three or more non-friends is similar.) Consider any three. If any two are friends, those two with the original person form a group where all three are friends. Therefore none of them may be friends. In that case, they are all non-friends so the condition is again satisfied.

The problem can also be thought of as a graph. Here the users are nodes. Each node is connected to every other. Each edge is coloured red (friends) or blue (strangers). Our theorem states that there is either a red triangle or a blue triangle. If we asked for there to be four nodes, all connected with identical colours, we need 18 nodes. That is as much as we know. For five nodes, we know that the answer is somewhere in between 43 and 49. Apart from that, we don't have a clue.

Van der Waerder's theorem

This is not the only problem in Ramsey theory. Van der Waerden's theorem states that if you have enough consecutive integers and you colour them with finitely many colours, you can find arbitrarily long arithmetic sequences with all numbers of the same colour. For an arithmetic sequence of length 2 we need 3 numbers. For 3 we need 9. For 4 we need 35. For 5 we need 178. Finally, for 6 we need 1132. After that, we must make do with lower bounds.

Graham's problem

Some problems in Ramsey theory are very hard to solve exactly. One example is Graham's problem. This is to find a number N, such that if a hypercube of N dimensions had all edges and diagonals coloured either red or blue, forming a complete graph of order 2^N,there will be 4 vertices such that they are all on the same plane and each line between them is the same colour. He found an upper bound that was roughly f_ω+1(64). This is known as Graham's number. It has since been reduced to a very large nested power tower. However, the lower bound is currently only 13. The difficulty is that we are dealing with graphs of 8192 nodes. We still can't check all configurations for graphs of 43 nodes. Also, it is very difficult to prove anything concrete without relying on horrendously large constructions.

Related entries

   • Graham's number